ttps://www.acmicpc.net/problem/12865
12865번: 평범한 배낭
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)
www.acmicpc.net
그리디를 하면 망해버립니다.
처음에 0-1 knapsack이란걸 모르다가, 이건 DP인것 같은데 DP를 어떻게 해야할까? 라는 고민을 했습니다.
그 다음에 했던건 그리디의 느낌으로..
1. 실패한 과정 (그리디)
Value 순으로 내림차순 정렬을 했습니다.
맨 위에부터 계속 value를 더합니다. 그다음 w도 누적으로 더해줍니다.
w가 초과되면, max에 현재 value를 넣고 다시 뭐 리셋하고 합니다. 머릿속으로는 최고 같습니다.

여기서 봅시다.
W| V
6 13
5 12
4 8
3 6
1. V 13선택, W는 6이다.
2. W 5 선택시, W는 11이라 안된다. 따라서 V = 12, W = 5로 다시 바꿔주고, MAX = 13
3. W 4 선택시, W는 9라서 안된다, 따라서 V = 8, W = 4로 다시 바꿔준다. MAX = 13 그대로
4. W 3 선택시, W는 7이라서 된닫. 따라서 V = 6+8 결국 MAX = 14
오잉? 될것같잖아?
이렇게 아름답게 순서가 나오면 됩니다. 하지만?
W|V (최대 무게 7kg라 가정)
1 150
2 50
17 40
4 35
처음에 1,2를 선택해서 max = 200이 됩니다.
하지만? 17을 만나면 앞에 1,2를 지워버리고 W = 17, V = 40으로 초기화 하기 때문에
맨 마지막 4kg를 더하지 못하고, Value가 200만 나와버립니다.
이런 문제때문에 결국엔 모든 과정을 다 봐야합니다.
0-1 knapsack은 다른 블로그들을 찾아보시길 바라겠습니다.
(표 그리기 이런거는 손으로 그리기가 힘들어서.. 미안합니다)
제가 이해한 내용은 다음과 같습니다.
***
제가 물품을 집었습니다.
if( 물품을 배낭에 넣을 수 있는가? == NO )
{
물품을 배낭에 넣지 않고, 최고의 가치를 지니는 배낭으로 선택
}else{ (물품을 배낭에 넣을 수 있는가? == YES)
max ( 물품을 배낭에 넣은 가치, 물품을 넣지 않았을때 최고의 가치를 지니는 배낭)
}
왜 max가 있는가?
가치가 -인 경우에는, 넣으면 손해입니다. 이런 경우도 제외 해야 합니다.
일단 가정이 이 전에 최고의 가치를 지니는 배낭만을 선택했다는 가정입니다.
그래야 이 식이 옳게 됩니다.
***
w = 수용할 수 있는 전체 무게
w_i = i번째의 무게
if( w < w_i ) // 수용할 수 있는 무게보다, i번째 물건의 무게가 더 나간다면
dp[i] = dp[ i-1, w ] // 지금의 물건을 제외하고, 이전까지의 배낭중에 최고의 가치를 갖는 배낭을 선택합니다.
else{ // i번째의 물건을 넣어도, 수용할 수 있는경우 ( 즉 배낭이 터지지 않는경우)
max( v_i + dp[i-1, w-w_i] , dp[i-1,w])
}
#include<cstdio>
#include<algorithm>
using namespace std;
typedef pair<int,int> ii;
ii bag[105];
int dp[103][100005];//40M..
int main(void)
{
int N,K;
int W,V;
scanf("%d %d",&N,&K);
for(int i = 1; i <= N; i++)
{
scanf("%d %d",&bag[i].first,&bag[i].second);
}
for(int i = 1; i <= N; i++)
{
for(int j = 1; j <= K; j++)
{
if( j < bag[i].first )// 전체무게 < 물품의 무게
{
dp[i][j] = dp[i-1][j];
}else{
dp[i][j] = max(bag[i].second + dp[i-1][j-bag[i].first], dp[i-1][j]);
}
}
}
printf("%d\n",dp[N][K]);
return 0;
}
이런식으로 나오게 될 것 입니다.
단점 : 메모리
최대 고를 수 있는 물품 N개와, 최대 나갈 수 있는 무게 K를 다 고려해야 해서 메모리 낭비가 심합니다.
특히나 sparse 할 경우에는 너무너무 끔찍합니다.
속도와 공간의 trade off라고 생각 합시다.
O( N+ K) 입니다. N은 물품 개수, K는 최대 무게
하지만, 때에 따라서 메모리를 정말 적게 쓰는 전략이 있습니다.
이 발상을 어떻게 했는지..
dp를 DP[N][W] = V로 생각하지 않습니다.
DP[W] = V 로 생각해서 해결했더라구요.
이게 어떻게 되긴 되더라구요.
아직 정확한 이유를 설명하지는 못하겠는데, 뭔가 위에서부터 채우다가, 아래의 값이 완성되면 i가 맨 마지막 index일때 최고의 값이 나오는? 이런 느낌입니다.
#include<cstdio>
#include<algorithm>
using namespace std;
typedef pair<int,int> ii;
ii bag[105];
int dp[100005];// dp[w]
int main(void)
{
int N,K;
int W,V;
int t;
int t2;
scanf("%d %d",&N,&K);
for(int i = 1; i <= N; i++)
{
scanf("%d %d",&bag[i].first,&bag[i].second);
}
for(int i = 1; i <= N; i++)
{
t2 = bag[i].first;
for(int j = K; j >= t2; j--)
{
t = dp[j-bag[i].first] + bag[i].second;
if( dp[j] < t)
dp[j] = t;
}
}
printf("%d\n",dp[K]);
return 0;
}위와 다른점은, j가 다릅니다
K부터 시작해서, W까지 갑니다.
왜 W까지만 가느냐?
dp[j - bag[i].first] 에서 bag[i].first가 j보다 더 크면 인덱스가 나가기 때문입니다.
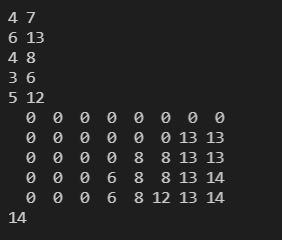
이건 예제로 한 번 보면 훨씬 이해가 쉽습니다
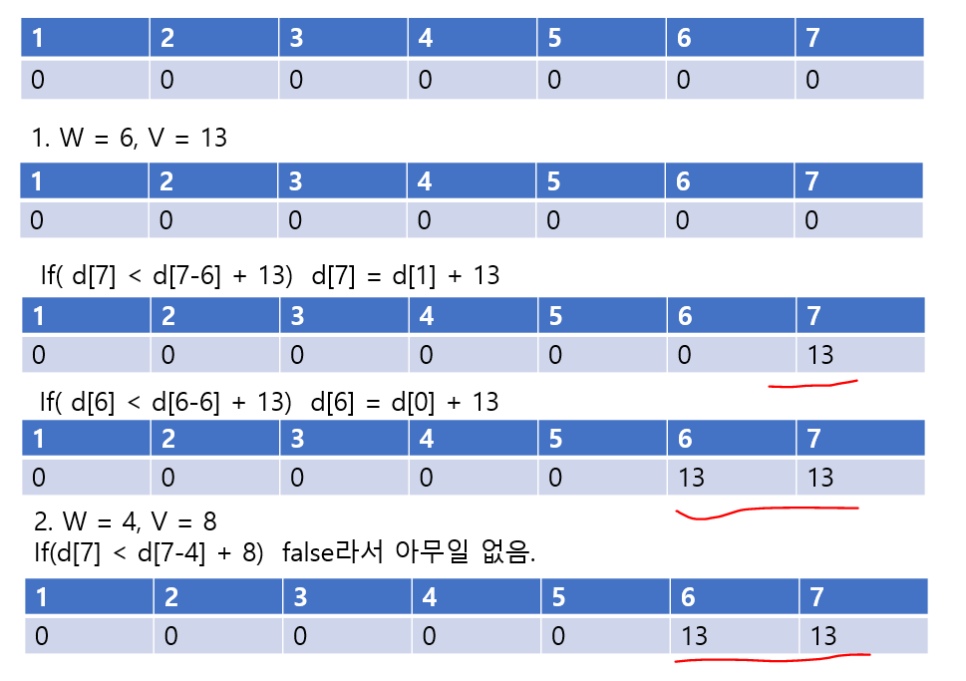
파워포인트로 만들다가 현기증 났습니다.
다들 무슨 느낌인지 아시겠죵^^?
여기서 핵심은..
이 발상을 어떻게 했는가?
저도 그게 궁금합니다.
이 문제를 보자마자 0-1 knapsack을 떠올리는 동시에 2차원 table이 머리속에 그려졌는데, 이게 비효율적인걸 캐치하면서 1차원으로 줄일 생각을 했다?
다음번엔 저도 도전해보겠습니다 ^^ 저는 이 발상을 못했거든요.
좋은 경험이었습니다^^

'컴퓨터 > 알고리즘' 카테고리의 다른 글
| [BOJ] 16926. 배열돌리기 1 (0) | 2021.08.30 |
|---|---|
| [Programmers] 2021 카카오 인턴십 2번 - 거리두기 확인하기 (0) | 2021.08.25 |
| [BOJ] 2579 계단오르기, C Macro function(매크로함수) (0) | 2021.07.26 |
| [BOJ] 1016. 제곱ㄴㄴ수 (에라토스테네스의 체) (0) | 2021.07.08 |
| [BOJ] 1080. 행렬 (0) | 2021.03.16 |


