728x90
반응형
https://www.acmicpc.net/problem/1016
1016번: 제곱 ㄴㄴ 수
어떤 수 X가 1보다 큰 제곱수로 나누어 떨어지지 않을 때, 제곱ㄴㄴ수라고 한다. 제곱수는 정수의 제곱이다. min과 max가 주어지면, min과 max를 포함한 사이에 제곱ㄴㄴ수가 몇 개 있는지 출력한다.
www.acmicpc.net
풀이방법 : 에라토스테네스의 체 + 약간의 조정 (제한시간 2초)
접근 :
가장 naive한 방법으로 생각해봤다.
for( i = 2; i <= sqrt(max) i ++){
for(j = min; j <= max; j++){
이렇게 하면 답은 찾을 수 있다. 모든 경우를 다 찾아보는것이다.
이렇게 되면 최악의 경우 10^6 * 10^6 = 10^12 = 약 1만 초 동안 돈다.
이거 돌린다음에 밥먹고, 씻고, 잠도 좀 자다가 커피도 마시고 오면 완성되어 있다. 하지만 제한시간은 2초이다. 타이트하게 2억번 이내로 찾는다고 생각해보자.
최적화 할 수 있는 부분 :
1. 첫번째 for문
에라토스테네스의 체 를 이용하면 굉장히 많은 중복을 제거할 수 있다.
이게 소수도 아닌데 갑자기 웬 에라토스냐? 할 수 있다.
4,9,16,25로 나누어 떨어지는거 찾는거 아니냐? 맞다.
근데 16은 4로도 나누어 떨어진다. 또한 625또한 25로 나누어 떨어진다.
위의 말이 이해가 되면 왜 체(sieve)를 통해서 걸러내는지 이해가 갈 것이다.
처음에 2의 배수인 4,6,8,10,12,14 이런식으로 쭉 걸러낸다.
좀만 생각해보면, 16,36,64,100,144 모두 2로 나누어 떨어진다.
따라서, [min,max]에서 2로 나누어 떨어진 부분은 다시 안봐도 된다는 뜻이다.
이런식으로 체로 걸러낼 수 있다.
이렇게 걸러내면 시간복잡도는 O(Nlog(logN)) 이라고 하는데(위키백과), 실제로 [1조, 1조100만] 으로 test 시에 280만번 정도의 반복횟수가 나왔다. 직접 재봤다.
그렇다면 280만회니까 약 300만이라고 치면 10^6 수준이므로, 나머지 [min,max] 최대 100만개에 해당하는 숫자들에서 나누어 떨어지는 수를 각 횟수당 100번정도 이내에 구해야 한다는 결론이 나온다. 이게 가능할까?
2. 두번째 for문
일단 난 316만번이 나왔다. (체 포함해서)

어떻게 했을까?
맨처음엔 시간초과가 났다
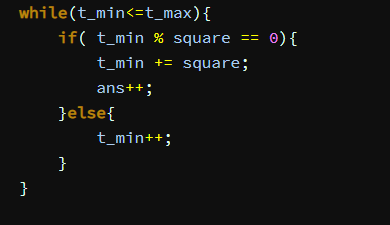
몇십억번 돌았던것 같은데.. 약간만 바꾸면 300만번에 가능하다.
1000 1004 1008
이런식으로 아래 for문에서도 체(sieve)를 사용하는 느낌으로 하면 된다.
위의 시간초과난 방식은 체를 사용하는 방식을 생각했는데도, else문 떄문에 시간초과가 난다.
나누어 떨어지는 수를 찾으라고 t_min++ 을 해줬는데, 이 찾는 과정이 코스트가 너무 비싸다.
조금만 생각하면 O(1)로 구해서, 깔끔하게 체를 쓸 수 있다.
코드를 보고 이해해보자.
#include<cstdio>
#include<cmath>
typedef long long int ll;
bool sieve[1000005];
bool checked[1000005];
using namespace std;
int main(void)
{
ll ans = 0;
ll min, max;
ll s_min, s_max;
scanf("%lld %lld",&min, &max);
s_min = (ll)(sqrt(min));
s_max = (ll)(sqrt(max));
ll square;
// 아래 최대 100만 10^6
// 위에 최대 100만, 위에는 10^2 안으로 줄여야함.
int cnt = 0;
for(ll i = 2; i <= s_max ; i++)
{
//printf("%d\n",sieve[i]);
if(sieve[i] == 1) continue;
square = i * i;
ll t_min = min;
ll t_max = max;
for(int k = i*2; k <= s_max; k+= i)
{
sieve[k] = 1;
cnt++;
}
//1000 1001 1002 1003 1004
//100 + ( 6 - (100%6)) == 최초 나누기 지점
ll t = square - (t_min % square);
if(t == square){
t = 0;
}
for(ll z = t+t_min; z <= max; z+= square){
if(!checked[z-min]) {
checked[z-min] = 1;
ans++;
cnt++;
}
}
}
printf("%d\n",cnt);
printf("%d\n", max-min+1-ans);
return 0;
}> ll t = square - (t_min % square);
이것만 이해하면 된다.
예시1)
100보다 큰 숫자에서 3으로 나누어 떨어지는 가장 가까운 수는?
102이다. 어떻게 구할까?
3 - ( 100 % 3) = 2
102는 가장 가까운 수다
예시2)
150보다 큰 숫자에서 13으로 나누어 떨어지는 가장 가까운 수는?
13 - (150 % 13) = 6
156이다.
이 방식을 통해서
바로 나누어 떨어지는 수를 구한후에, 1000 , 1004, 1008 이런식으로 가게 했다.
이렇게 하면 4일때 약 25만번,, 10일때 1000번 .. 100일때 더 적은숫자..
이런식으로 해서 310만번 안에 할 수 있다.
에라토스테네스의 체가 이해가 안가면.. 여기 설명 기가 막히다. 그림 보면 딱 느낌이 올 것이다.
https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes
Sieve of Eratosthenes - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Ancient algorithm for generating prime numbers Sieve of Eratosthenes: algorithm steps for primes below 121 (including optimization of starting from prime's square). In mathematics, the
en.wikipedia.org
오늘도 열정으로...

728x90
반응형
'컴퓨터 > 알고리즘' 카테고리의 다른 글
| [BOJ] 12865. 평범한 배낭(0-1 knapsack) (0) | 2021.08.20 |
|---|---|
| [BOJ] 2579 계단오르기, C Macro function(매크로함수) (0) | 2021.07.26 |
| [BOJ] 1080. 행렬 (0) | 2021.03.16 |
| [BOJ] 2573 빙산 (0) | 2021.02.23 |
| [SWEA] 9700. USB 꽂기의 미스터리 (문제 꼼꼼히 읽어야하는 이유) (0) | 2021.02.20 |



